
Gambler's Fallacy — Why Not Reversed Gambler's Fallacy As Well?
By Ion Saliu, ★ Founder of Gambling Mathematics



Let's consider an event with probability of success p and probability of failure q = 1 - p. As far as I know, the probability of n consecutive successes or failures is expressed as p ^ n or q ^ n.
Even from high school I know that the limit of q ^ n when n tends to infinity is 0 if -1<q<1. That would mean that the probability of an infinite success or failure is 0. Conversely, it is certain that this will not occur. Are my thoughts correct?
The gambler's fallacy is mostly advocated by those who have a vested interest: CASINOS. That might even infer “legitimacy” of cheating by the casino personnel! You only hear that the gambler is fated to lose… to lose forever, that is!
In truth, you play roulette, flat-betting: You are fated to lose at a rate of around 5.26% of the time. If they say you are going to lose infinity of times — the reverse is also TRUE. But can you expect to WIN infinity of times? NOT! But you won't hear those advocates claiming the reversed gambler's fallacy: Win forever, gambler!
If you look at the image of roulette spins, there are losers, and there winners... but very close to what probability theory formulas calculate. Nothing comes even close to those mathematical aberrations with gambling fallacy in their names:
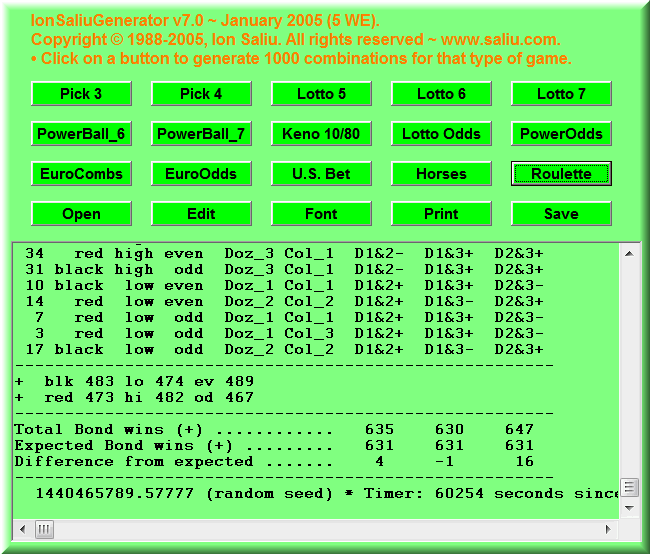
This gambler's fallacy thing is the weapon they fire at me more intensely lately. They ain't got anything else but that pathetic slogan. They aim at the Fundamental Formula of Gambling I advocate. It is not only probability, p. There are also two more fundamental elements: The number of trials, N, and the degree of certainty, DC.
You can expect, knowingly, to lose 4-5 times in a row in some 100 trials (roulette spins, blackjack hands, etc.). Equivalently, you can expect to register streaks of 4-5 consecutive wins. That's what makes the casinos mouth-foam in desperate anger. I did experience that in 2003, in Atlantic City. The surprise to me was the screamer. She was a simple roulette dealer, who did not benefit directly from a gambler's loss! Actually, she would have benefited only from a friendly reaction to me: I would have tipped her! In that case, I didn't give her a dime! But I tipped generously the waitress! BRRRRRRRRAHAHAHAHA!!!!!!!
The debates are good if conducted bona fide.
“Personally I see no way how I can consistently estimate the exact moments or even a finite interval favorable for a bet increase… “
The real fallacy here is your belief (and those vested advocates of gambler's fallacy): absolute certainty. There is NO absolute certainty in the Universe. But things follow the rules of randomness. There are skips and streaks. Don't you tell me that you had an infinite number of losses (L) in a row; or that you've never won more than once… that is, never streaks of 2 or longer wins (W)!
If an honest individual, just write down everything at the roulette table, or the blackjack table. You will see very clearly the streaks (WWW or LLL)… Furthermore, you can see that the streaks follow mathematical formulas. The longer the streak, the rarer it occurs. The gambler fallacists (sounds like fascists, yeah!) would always tell you that the longest possible losing streak has the same chance as a single losing streak! Now, that ends any bona fide debate, because the Earth is not flat. And, yes, there is a degree of certainty greater than zero for Moon to collide with Earth! If worrying about that, no human could survive...
It's all mathematical, axiomatic one! Nothing escapes mathematics, from the tiniest atoms in your blood to the most gigantic galaxies. That's the reason why I loudly say: “God fears mathematics, while Einstein hates gambling.” And thusly Fundamental Formula of Gambling makes it loud and clear (undeniable, that is):

 Back to Forums Index Socrates Home Search
Back to Forums Index Socrates Home Search
